矩阵乘法
在本教程中,您将编写一个非常简短的高性能 FP16 矩阵乘法内核,其性能可以与 cuBLAS 或 rocBLAS 相媲美。
您将具体学习以下内容:
- 块级矩阵乘法。
- 多维指针算术。
- 为提高 L2 缓存命中率而进行的程序重排序。
- 自动性能调优。
动机
矩阵乘法是现代大多数高性能计算系统的关键构建块。
矩阵乘法难以优化,因此其实现通常由硬件供应商自行完成,作为所谓「内核库」(例如 cuBLAS )的一部分。
这些库通常是专有的,不能轻易定制以满足现代深度学习工作负载的需求(例如融合激活函数)。
在本教程中,您将学习如何借助一种更易于定制和扩展的方法,用 Triton 实现高效的矩阵乘法。
整体来说,我们将编写的内核将实现以下的分块算法,用于计算一个 (M, K) 乘以一个 (K, N) 的矩阵:
# Do in parallel
# 并行进行
for m in range(0, M, BLOCK_SIZE_M):
# Do in parallel
# 并行进行
for n in range(0, N, BLOCK_SIZE_N):
acc = zeros((BLOCK_SIZE_M, BLOCK_SIZE_N), dtype=float32)
for k in range(0, K, BLOCK_SIZE_K):
a = A[m : m+BLOCK_SIZE_M, k : k+BLOCK_SIZE_K]
b = B[k : k+BLOCK_SIZE_K, n : n+BLOCK_SIZE_N]
acc += dot(a, b)
C[m : m+BLOCK_SIZE_M, n : n+BLOCK_SIZE_N] = acc
其中,每次双重嵌套的循环迭代都由专用的 Triton 程序实例执行。
计算内核
实际上,上述算法在 Triton 中实现起来相当简单。
主要困难在于计算内循环中必须读取 A 和 B 块的内存位置。为此,我们需要多维指针算术。
指针算术
因此,对于行主序的二维张量 X,X[i, j] 的内存位置由 &X[i, j] = X + i*stride_xi + j*stride_xj 给出。
因此,A[m : m+BLOCK_SIZE_M, k:k+BLOCK_SIZE_K]和B[k : k+BLOCK_SIZE_K, n:n+BLOCK_SIZE_N] 的指针块可以用伪代码定义为:
&A[m : m+BLOCK_SIZE_M, k:k+BLOCK_SIZE_K] = a_ptr + (m : m+BLOCK_SIZE_M)[:, None]*A.stride(0) + (k : k+BLOCK_SIZE_K)[None, :]*A.stride(1);
&B[k : k+BLOCK_SIZE_K, n:n+BLOCK_SIZE_N] = b_ptr + (k : k+BLOCK_SIZE_K)[:, None]*B.stride(0) + (n : n+BLOCK_SIZE_N)[None, :]*B.stride(1);
这意味着在 Triton 中可以将 A 和 B 块的指针初始化(即 k=0 )为以下代码。还要注意,当 M 不是 BLOCK_SIZE_M 的倍数或 N 不是 BLOCK_SIZE_N 的倍数时,我们需要额外的取模运算来应对,这种情况下我们可以用一些无用的值填充数据,这些值不会对结果有影响。对于 K 维度,我们将在后面使用掩码加载语义来处理。
offs_am = (pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)) % M
offs_bn = (pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)) % N
offs_k = tl.arange(0, BLOCK_SIZE_K)
a_ptrs = a_ptr + (offs_am[:, None]*stride_am + offs_k [None, :]*stride_ak)
b_ptrs = b_ptr + (offs_k [:, None]*stride_bk + offs_bn[None, :]*stride_bn)
然后在内循环中更新如下:
a_ptrs += BLOCK_SIZE_K * stride_ak;
b_ptrs += BLOCK_SIZE_K * stride_bk;
L2 缓存优化
正如上面提到的,每个程序实例计算 C 的一个 [BLOCK_SIZE_M, BLOCK_SIZE_N] 块。
重点要记住这些块的计算顺序,因为它会影响我们程序的 L2 缓存命中率,而且,简单的行主序排序是行不通的。
pid = tl.program_id(axis=0)
grid_n = tl.cdiv(N, BLOCK_SIZE_N)
pid_m = pid // grid_n
pid_n = pid % grid_n
一种可能的解决方案是以促进数据重用的顺序启动块。
在转向下一列之前,可以通过将 GROUP_M 行的块进行「超级分组」来实现此目的:
# Program ID
# 程序 ID
pid = tl.program_id(axis=0)
# Number of program ids along the M axis
# M 轴上程序 id 的数量
num_pid_m = tl.cdiv(M, BLOCK_SIZE_M)
# Number of programs ids along the N axis
# N 轴上程序 id 的数量
num_pid_n = tl.cdiv(N, BLOCK_SIZE_N)
# Number of programs in group
# 组中程序数量
num_pid_in_group = GROUP_SIZE_M * num_pid_n
# Id of the group this program is in
# 本程序所在的组 id
group_id = pid // num_pid_in_group
# Row-id of the first program in the group
# 组内第一个程序的行 id
first_pid_m = group_id * GROUP_SIZE_M
# If `num_pid_m` isn't divisible by `GROUP_SIZE_M`, the last group is smaller
# 如果 `num_pid_m` 不能被 `GROUP_SIZE_M` 整除,最后一组会比较小
group_size_m = min(num_pid_m - first_pid_m, GROUP_SIZE_M)
# *Within groups*, programs are ordered in a column-major order
# 在组内,程序按列主序排序。
# Row-id of the program in the *launch grid*
# 启动网格中程序的行 id
pid_m = first_pid_m + ((pid % num_pid_in_group) % group_size_m)
# Col-id of the program in the *launch grid*
# 启动网格中程序的列 id
pid_n = (pid % num_pid_in_group) // group_size_m
例如,在以下的矩阵乘法示例中,每个矩阵都是 9*9 个块。可以看到,如果按行主序计算输出,我们需要加载 90 个块到 SRAM 中来计算前 9 个输出块,但如果按组顺序计算,我们只需要加载 54 个块。
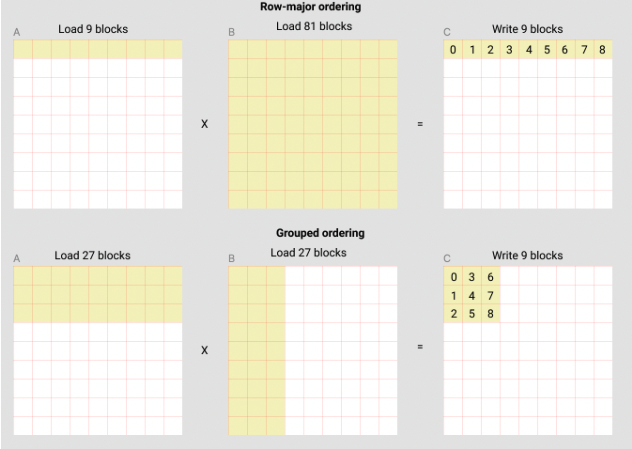
实际上,这种做法可以在某些硬件架构上显著提升我们的矩阵乘法核心性能,例如在 A100 上,性能提升可以超过 10%,从 220 到 245 TFLOPS 不等。
最终结果
import torch
import triton
import triton.language as tl
def is_cuda():
return triton.runtime.driver.active.get_current_target().backend == "cuda"
def is_hip_mi200():
target = triton.runtime.driver.active.get_current_target()
return target.backend == 'hip' and target.arch == 'gfx90a'
def get_cuda_autotune_config():
return [
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 256, 'BLOCK_SIZE_K': 64, 'GROUP_SIZE_M': 8}, num_stages=3,
num_warps=8),
triton.Config({'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 256, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 64, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 32, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 32, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=5,
num_warps=2),
triton.Config({'BLOCK_SIZE_M': 32, 'BLOCK_SIZE_N': 64, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=5,
num_warps=2),
# Good config for fp8 inputs.
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 256, 'BLOCK_SIZE_K': 128, 'GROUP_SIZE_M': 8}, num_stages=3,
num_warps=8),
triton.Config({'BLOCK_SIZE_M': 256, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 128, 'GROUP_SIZE_M': 8}, num_stages=3,
num_warps=8),
triton.Config({'BLOCK_SIZE_M': 256, 'BLOCK_SIZE_N': 64, 'BLOCK_SIZE_K': 128, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 256, 'BLOCK_SIZE_K': 128, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 128, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 64, 'BLOCK_SIZE_K': 64, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 64, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 32, 'BLOCK_SIZE_K': 64, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4)
]
def get_hip_autotune_config():
return [
triton.Config(
{'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 256, 'BLOCK_SIZE_K': 16, 'GROUP_SIZE_M': 1, 'waves_per_eu': 2},
num_warps=4, num_stages=0),
triton.Config(
{'BLOCK_SIZE_M': 256, 'BLOCK_SIZE_N': 256, 'BLOCK_SIZE_K': 16, 'GROUP_SIZE_M': 4, 'waves_per_eu': 2},
num_warps=8, num_stages=0),
triton.Config(
{'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 1, 'waves_per_eu': 2},
num_warps=8, num_stages=0),
triton.Config(
{'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8, 'waves_per_eu': 3},
num_warps=4, num_stages=0),
triton.Config(
{'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 64, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 1, 'waves_per_eu': 8},
num_warps=4, num_stages=0),
]
def get_autotune_config():
if is_cuda():
return get_cuda_autotune_config()
else:
return get_hip_autotune_config()
# `triton.jit`'ed functions can be auto-tuned by using the `triton.autotune` decorator, which consumes:
# `triton.jit` 函数可以通过使用 `triton.autotune` 装饰器进行自动调优,该装饰器接受以下内容:
# - A list of `triton.Config` objects that define different configurations of
# meta-parameters (e.g., `BLOCK_SIZE_M`) and compilation options (e.g., `num_warps`) to try
# - 一组 `triton.Config` 对象的列表,这些对象定义了不同的元参数配置(例如 `BLOCK_SIZE_M`)和编译选项(例如 `num_warps`)以供尝试。
# - An auto-tuning *key* whose change in values will trigger evaluation of all the
# provided configs
# - 一个自动调优的 key,其值的变化将触发对所有提供的配置进行评估。
@triton.autotune(
configs=get_autotune_config(),
key=['M', 'N', 'K'],
)
@triton.jit
def matmul_kernel(
# Pointers to matrices
# 矩阵指针
a_ptr, b_ptr, c_ptr,
# Matrix dimensions
# 矩阵维度
M, N, K,
# The stride variables represent how much to increase the ptr by when moving by 1
# element in a particular dimension. E.g. `stride_am` is how much to increase `a_ptr`
# by to get the element one row down (A has M rows).
# 这些步幅变量表示在特定维度移动 1 个元素时,`ptr` 应该增加多少。例如,`stride_am` 指示了为了访问下一行的元素(假设 `A` 有 `M` 行),需要增加多少 `a_ptr`。
stride_am, stride_ak, #
stride_bk, stride_bn, #
stride_cm, stride_cn,
# Meta-parameters
# 元参数
BLOCK_SIZE_M: tl.constexpr, BLOCK_SIZE_N: tl.constexpr, BLOCK_SIZE_K: tl.constexpr, #
GROUP_SIZE_M: tl.constexpr, #
ACTIVATION: tl.constexpr #
):
"""Kernel for computing the matmul C = A x B.
A has shape (M, K), B has shape (K, N) and C has shape (M, N)
"""
"""计算矩阵乘法 C = A x B 的核心算法。
其中,A 的形状为 (M, K),B 的形状为 (K, N),C 的形状为 (M, N)。
"""
# -----------------------------------------------------------
# Map program ids `pid` to the block of C it should compute.
# 将程序 ID `pid` 映射到它应计算的 C 块。
# This is done in a grouped ordering to promote L2 data reuse.
# 这是按组顺序进行的,以促进 L2 数据重用。
# See above `L2 Cache Optimizations` section for details.
# 详细信息请参见上述的 `L2 缓存优化` 部分。
pid = tl.program_id(axis=0)
num_pid_m = tl.cdiv(M, BLOCK_SIZE_M)
num_pid_n = tl.cdiv(N, BLOCK_SIZE_N)
num_pid_in_group = GROUP_SIZE_M * num_pid_n
group_id = pid // num_pid_in_group
first_pid_m = group_id * GROUP_SIZE_M
group_size_m = min(num_pid_m - first_pid_m, GROUP_SIZE_M)
pid_m = first_pid_m + ((pid % num_pid_in_group) % group_size_m)
pid_n = (pid % num_pid_in_group) // group_size_m
# ----------------------------------------------------------
# Create pointers for the first blocks of A and B.
# 创建 A 和 B 第一个块的指针
# We will advance this pointer as we move in the K direction
# and accumulate
# 在沿着 K 方向移动时,我们将推进这个指针并累加
# `a_ptrs` is a block of [BLOCK_SIZE_M, BLOCK_SIZE_K] pointers
# `a_ptrs` 是一个 [BLOCK_SIZE_M, BLOCK_SIZE_K] 大小的指针块
# `b_ptrs` is a block of [BLOCK_SIZE_K, BLOCK_SIZE_N] pointers
# `b_ptrs` 是一个 [BLOCK_SIZE_K, BLOCK_SIZE_N] 大小的指针块
# See above `Pointer Arithmetic` section for details
# 详细信息请参见上述的 `指针算术` 部分。
offs_am = (pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)) % M
offs_bn = (pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)) % N
offs_k = tl.arange(0, BLOCK_SIZE_K)
a_ptrs = a_ptr + (offs_am[:, None] * stride_am + offs_k[None, :] * stride_ak)
b_ptrs = b_ptr + (offs_k[:, None] * stride_bk + offs_bn[None, :] * stride_bn)
# -----------------------------------------------------------
# Iterate to compute a block of the C matrix.
# 迭代计算 C 矩阵的一个块。
# We accumulate into a `[BLOCK_SIZE_M, BLOCK_SIZE_N]` block
# of fp32 values for higher accuracy.
# 我们累加到一个 `[BLOCK_SIZE_M, BLOCK_SIZE_N]` 大小的 fp32 值块,以提高精度。
# `accumulator` will be converted back to fp16 after the loop.
# `accumulator` 在循环结束后将转换回 fp16。
accumulator = tl.zeros((BLOCK_SIZE_M, BLOCK_SIZE_N), dtype=tl.float32)
for k in range(0, tl.cdiv(K, BLOCK_SIZE_K)):
# Load the next block of A and B, generate a mask by checking the K dimension.
# 加载 A 和 B 的下一个块,通过检查 K 维度生成一个掩码。
# If it is out of bounds, set it to 0.
# 如果超出边界设为 0
a = tl.load(a_ptrs, mask=offs_k[None, :] < K - k * BLOCK_SIZE_K, other=0.0)
b = tl.load(b_ptrs, mask=offs_k[:, None] < K - k * BLOCK_SIZE_K, other=0.0)
# We accumulate along the K dimension.
# 通过着 K 维度进行累加。
accumulator = tl.dot(a, b, accumulator)
# Advance the ptrs to the next K block.
# 指针前进到下一个 K 块。
a_ptrs += BLOCK_SIZE_K * stride_ak
b_ptrs += BLOCK_SIZE_K * stride_bk
# You can fuse arbitrary activation functions here
# while the accumulator is still in FP32!
# 在累加器仍然是 FP32 的情况下,您可以在这里融合任意激活函数!
if ACTIVATION == "leaky_relu":
accumulator = leaky_relu(accumulator)
c = accumulator.to(tl.float16)
# -----------------------------------------------------------
# Write back the block of the output matrix C with masks.
# 写回带有掩码的输出矩阵 C 的块。
offs_cm = pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)
offs_cn = pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)
c_ptrs = c_ptr + stride_cm * offs_cm[:, None] + stride_cn * offs_cn[None, :]
c_mask = (offs_cm[:, None] < M) & (offs_cn[None, :] < N)
tl.store(c_ptrs, c, mask=c_mask)
# We can fuse `leaky_relu` by providing it as an `ACTIVATION` meta-parameter in `matmul_kernel`.
# 我们可以通过在 `matmul_kernel` 中将 `leaky_relu` 作为 `ACTIVATION` 元参数来融合 `leaky_relu`。
@triton.jit
def leaky_relu(x):
return tl.where(x >= 0, x, 0.01 * x)
现在我们可以创建一个方便的 wrapper 函数,只接受两个输入张量,并且:(1) 检查任何 shape 约束;(2) 分配输出;(3) 启动上述的内核。
def matmul(a, b, activation=""):
# Check constraints.
# 检查约束
assert a.shape[1] == b.shape[0], "Incompatible dimensions"
assert a.is_contiguous(), "Matrix A must be contiguous"
M, K = a.shape
K, N = b.shape
# Allocates output.
# 分配输出
c = torch.empty((M, N), device=a.device, dtype=torch.float16)
# 1D launch kernel where each block gets its own program.
# 1 维启动核心,其中每个块都有自己的程序。
grid = lambda META: (triton.cdiv(M, META['BLOCK_SIZE_M']) * triton.cdiv(N, META['BLOCK_SIZE_N']), )
matmul_kernel[grid](
a, b, c, #
M, N, K, #
a.stride(0), a.stride(1), #
b.stride(0), b.stride(1), #
c.stride(0), c.stride(1), #
ACTIVATION=activation #
)
return c
单元测试
对自定义矩阵乘法操作进行测试,与 原生 torch 实现(例如 cuBLAS)进行对比。
torch.manual_seed(0)
a = torch.randn((512, 512), device='cuda', dtype=torch.float16)
b = torch.randn((512, 512), device='cuda', dtype=torch.float16)
triton_output = matmul(a, b)
torch_output = torch.matmul(a, b)
print(f"triton_output_with_fp16_inputs={triton_output}")
print(f"torch_output_with_fp16_inputs={torch_output}")
# Bigger tolerance for AMD MI200 devices.
# 对于 AMD MI200 设备,使用更大的容差。
# MI200 devices use reduced precision fp16 and bf16 and flush input and
# output denormal values to zero. Detailed info is at: https://pytorch.org/docs/stable/notes/numerical_accuracy.html#reduced-precision-fp16-and-bf16-gemms-and-convolutions-on-amd-instinct-mi200-devices
# MI200 设备使用降低精度的 FP16 和 BF16,并将输入和输出的非规格化值清零。详细信息在以下链接:https://pytorch.org/docs/stable/notes/numerical_accuracy.html#reduced-precision-fp16-and-bf16-gemms-and-convolutions-on-amd-instinct-mi200-devices
rtol = 1e-2 if is_hip_mi200() else 0
if torch.allclose(triton_output, torch_output, atol=1e-2, rtol=rtol):
print("✅ Triton and Torch match")
else:
print("❌ Triton and Torch differ")
TORCH_HAS_FP8 = hasattr(torch, "float8_e5m2")
if TORCH_HAS_FP8 and is_cuda():
torch.manual_seed(0)
a = torch.randn((512, 512), device="cuda", dtype=torch.float16)
b = torch.randn((512, 512), device="cuda", dtype=torch.float16)
a = a.to(torch.float8_e5m2)
# pre-transpose b for efficiency.
# 提前转置 b 提高效率
b = b.T
b = b.to(torch.float8_e5m2)
triton_output = matmul(a, b)
torch_output = torch.matmul(a.to(torch.float16), b.to(torch.float16))
print(f"triton_output_with_fp8_inputs={triton_output}")
print(f"torch_output_with_fp8_inputs={torch_output}")
if torch.allclose(triton_output, torch_output, atol=0.125, rtol=0):
print("✅ Triton and Torch match")
else:
print("❌ Triton and Torch differ")
Out:
triton_output_with_fp16_inputs=tensor([[-10.9531, -4.7109, 15.6953, ..., -28.4062, 4.3320, -26.4219],
[ 26.8438, 10.0469, -5.4297, ..., -11.2969, -8.5312, 30.7500],
[-13.2578, 15.8516, 18.0781, ..., -21.7656, -8.6406, 10.2031],
...,
[ 40.2812, 18.6094, -25.6094, ..., -2.7598, -3.2441, 41.0000],
[ -6.1211, -16.8281, 4.4844, ..., -21.0312, 24.7031, 15.0234],
[-17.0938, -19.0000, -0.3831, ..., 21.5469, -30.2344, -13.2188]],
device='cuda:0', dtype=torch.float16)torch_output_with_fp16_inputs=tensor([[-10.9531, -4.7109, 15.6953, ..., -28.4062, 4.3320, -26.4219],
[ 26.8438, 10.0469, -5.4297, ..., -11.2969, -8.5312, 30.7500],
[-13.2578, 15.8516, 18.0781, ..., -21.7656, -8.6406, 10.2031],
...,
[ 40.2812, 18.6094, -25.6094, ..., -2.7598, -3.2441, 41.0000],
[ -6.1211, -16.8281, 4.4844, ..., -21.0312, 24.7031, 15.0234],
[-17.0938, -19.0000, -0.3831, ..., 21.5469, -30.2344, -13.2188]], device='cuda:0', dtype=torch.float16)✅ Triton and Torch matchtriton_output_with_fp8_inputs=tensor([[-21.4375, 13.1719, 6.0352, ..., 28.7031, 8.6719, -40.7500],
[ 10.0000, 37.0000, -5.5664, ..., 20.9844, 46.8125, 30.8281],
[ 19.5625, -3.0078, -20.0469, ..., -2.1309, -8.0625, 12.5625],
...,
[-18.1562, -34.1562, -27.4219, ..., -27.3906, -24.0938, -12.3516],
[ -3.3945, -8.6250, -23.6562, ..., -4.1094, -3.5332, -16.0781],
[-23.9688, -3.2637, -33.6875, ..., 17.3125, -36.6250, 25.8594]], device='cuda:0', dtype=torch.float16)torch_output_with_fp8_inputs=tensor([[-21.4375, 13.1719, 6.0352, ..., 28.7031, 8.6719, -40.7500],
[ 10.0000, 37.0000, -5.5664, ..., 20.9844, 46.8125, 30.8281],
[ 19.5625, -3.0078, -20.0469, ..., -2.1309, -8.0625, 12.5625],
...,
[-18.1562, -34.1562, -27.4219, ..., -27.3906, -24.0938, -12.3516],
[ -3.3945, -8.6250, -23.6562, ..., -4.1094, -3.5332, -16.0781],
[-23.9688, -3.2637, -33.6875, ..., 17.3125, -36.6250, 25.8594]], device='cuda:0', dtype=torch.float16)✅ Triton and Torch match
基准测试
比较内核与 cuBLAS 或 rocBLAS 的性能差异。此处以方阵为例进行讲解,也可以可以按需调整脚本,对其他 matrix shape 进行基准测试。
ref_lib = 'cuBLAS' if is_cuda() else 'rocBLAS'
configs = []
for fp8_inputs in [False, True]:
if fp8_inputs and (not TORCH_HAS_FP8 or not is_cuda()):
continue
configs.append(
triton.testing.Benchmark(
x_names=["M", "N", "K"], # Argument names to use as an x-axis for the plot 作为绘图 x 轴的参数名
x_vals=[128 * i for i in range(2, 33)], # Different possible values for `x_name` `x_names` 参数的不同可能值
line_arg="provider", # Argument name whose value corresponds to a different line in the plot 对应绘图中不同线的参数名
# Possible values for `line_arg` `line_arg` 的可能值
# Don't compare to cublas for fp8 cases as torch.matmul doesn't support fp8 at the moment. 在 fp8 情况下不与 cuBLAS 比较,因为 torch.matmul 目前不支持 fp8。
line_vals=["triton"] if fp8_inputs else [ref_lib.lower(), "triton"], # Label name for the lines
line_names=["Triton"] if fp8_inputs else [ref_lib, "Triton"], # Line styles
styles=[("green", "-"), ("blue", "-")],
ylabel="TFLOPS", # Label name for the y-axis y 轴的标签名称
plot_name="matmul-performance-" +
("fp16" if not fp8_inputs else "fp8"), # Name for the plot, used also as a file 绘图名称,也用作保存绘图的文件名 name for saving the plot.
args={"fp8_inputs": fp8_inputs},
))
@triton.testing.perf_report(configs)
def benchmark(M, N, K, provider, fp8_inputs):
a = torch.randn((M, K), device='cuda', dtype=torch.float16)
b = torch.randn((K, N), device='cuda', dtype=torch.float16)
if TORCH_HAS_FP8 and fp8_inputs:
a = a.to(torch.float8_e5m2)
b = b.T
b = b.to(torch.float8_e5m2)
quantiles = [0.5, 0.2, 0.8]
if provider == ref_lib.lower():
ms, min_ms, max_ms = triton.testing.do_bench(lambda: torch.matmul(a, b), quantiles=quantiles)
if provider == 'triton':
ms, min_ms, max_ms = triton.testing.do_bench(lambda: matmul(a, b), quantiles=quantiles)
perf = lambda ms: 2 * M * N * K * 1e-12 / (ms * 1e-3)
return perf(ms), perf(max_ms), perf(min_ms)
benchmark.run(show_plots=True, print_data=True)
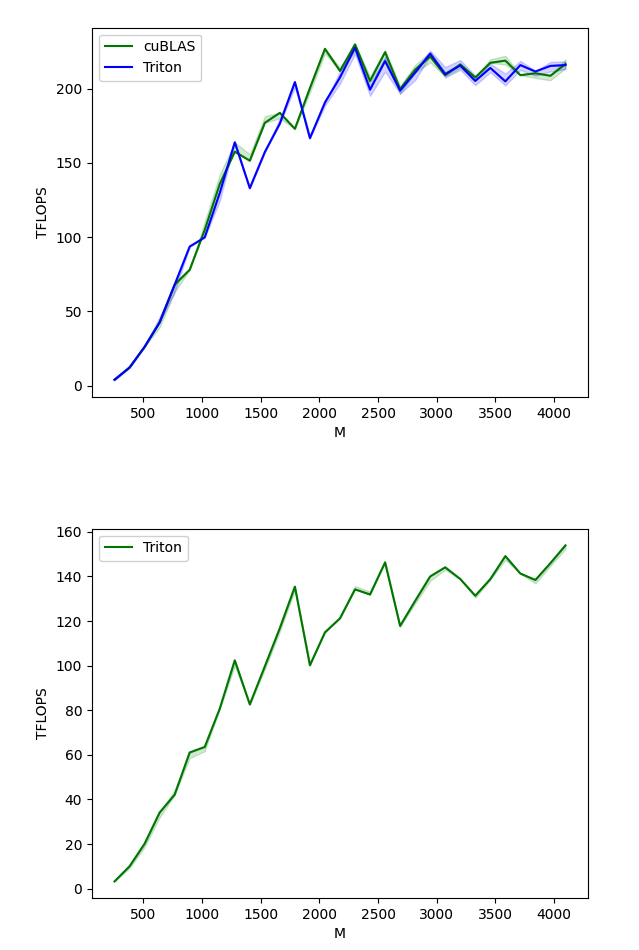
Out:
matmul-performance-fp16:
| M | N | K | cuBLAS | Triton | |
|---|---|---|---|---|---|
| 0 | 256.0 | 256.0 | 256.0 | 4.096 | 4.096 |
| 1 | 384.0 | 384.0 | 384.0 | 12.288 | 12.288 |
| 2 | 512.0 | 512.0 | 512.0 | 26.214401 | 26.214401 |
| 3 | 640.0 | 640.0 | 640.0 | 42.666665 | 42.666665 |
| 4 | 768.0 | 768.0 | 768.0 | 68.056616 | 68.056616 |
| 5 | 896.0 | 896.0 | 896.0 | 78.051553 | 93.661869 |
| 6 | 1024.0 | 1024.0 | 1024.0 | 104.857603 | 99.864382 |
| 7 | 1152.0 | 1152.0 | 1152.0 | 135.726544 | 129.825388 |
| 8 | 1280.0 | 1280.0 | 1280.0 | 157.538463 | 163.840004 |
| 9 | 1408.0 | 1408.0 | 1408.0 | 151.438217 | 132.970149 |
| 10 | 1536.0 | 1536.0 | 1536.0 | 176.947204 | 157.286398 |
| 11 | 1664.0 | 1664.0 | 1664.0 | 183.651271 | 176.449258 |
| 12 | 1792.0 | 1792.0 | 1792.0 | 172.914215 | 204.353162 |
| 13 | 1920.0 | 1920.0 | 1920.0 | 200.347822 | 166.554219 |
| 14 | 2048.0 | 2048.0 | 2048.0 | 226.719125 | 190.650180 |
| 15 | 2176.0 | 2176.0 | 2176.0 | 211.827867 | 207.460296 |
| 16 | 2304.0 | 2304.0 | 2304.0 | 229.691080 | 227.503545 |
| 17 | 2432.0 | 2432.0 | 2432.0 | 205.069087 | 199.251522 |
| 18 | 2560.0 | 2560.0 | 2560.0 | 224.438347 | 218.453323 |
| 19 | 2688.0 | 2688.0 | 2688.0 | 199.647657 | 198.602388 |
| 20 | 2816.0 | 2816.0 | 2816.0 | 212.752230 | 210.696652 |
| 21 | 2944.0 | 2944.0 | 2944.0 | 221.493479 | 223.479969 |
| 22 | 3072.0 | 3072.0 | 3072.0 | 208.941345 | 209.715208 |
| 23 | 3200.0 | 3200.0 | 3200.0 | 216.216207 | 215.488222 |
| 24 | 3328.0 | 3328.0 | 3328.0 | 207.467716 | 205.103410 |
| 25 | 3456.0 | 3456.0 | 3456.0 | 217.308808 | 213.850319 |
| 26 | 3584.0 | 3584.0 | 3584.0 | 218.772251 | 204.818663 |
| 27 | 3712.0 | 3712.0 | 3712.0 | 208.990259 | 215.761000 |
| 28 | 3840.0 | 3840.0 | 3840.0 | 210.250955 | 211.456969 |
| 29 | 3968.0 | 3968.0 | 3968.0 | 208.587935 | 215.209760 |
| 30 | 4096.0 | 4096.0 | 4096.0 | 216.480204 | 215.784121 |
matmul-performance-fp8:
| M | N | K | Triton | |
|---|---|---|---|---|
| 0 | 256.0 | 256.0 | 256.0 | 3.276800 |
| 1 | 384.0 | 384.0 | 384.0 | 10.053818 |
| 2 | 512.0 | 512.0 | 512.0 | 20.164923 |
| 3 | 640.0 | 640.0 | 640.0 | 34.133334 |
| 4 | 768.0 | 768.0 | 768.0 | 42.130286 |
| 5 | 896.0 | 896.0 | 896.0 | 61.083825 |
| 6 | 1024.0 | 1024.0 | 1024.0 | 63.550060 |
| 7 | 1152.0 | 1152.0 | 1152.0 | 80.702267 |
| 8 | 1280.0 | 1280.0 | 1280.0 | 102.400003 |
| 9 | 1408.0 | 1408.0 | 1408.0 | 82.602666 |
| 10 | 1536.0 | 1536.0 | 1536.0 | 99.688560 |
| 11 | 1664.0 | 1664.0 | 1664.0 | 116.868992 |
| 12 | 1792.0 | 1792.0 | 1792.0 | 135.414749 |
| 13 | 1920.0 | 1920.0 | 1920.0 | 100.173911 |
| 14 | 2048.0 | 2048.0 | 2048.0 | 114.912434 |
| 15 | 2176.0 | 2176.0 | 2176.0 | 121.226797 |
| 16 | 2304.0 | 2304.0 | 2304.0 | 134.201527 |
| 17 | 2432.0 | 2432.0 | 2432.0 | 131.898888 |
| 18 | 2560.0 | 2560.0 | 2560.0 | 146.285712 |
| 19 | 2688.0 | 2688.0 | 2688.0 | 117.804519 |
| 20 | 2816.0 | 2816.0 | 2816.0 | 129.036114 |
| 21 | 2944.0 | 2944.0 | 2944.0 | 139.988852 |
| 22 | 3072.0 | 3072.0 | 3072.0 | 144.079147 |
| 23 | 3200.0 | 3200.0 | 3200.0 | 138.828637 |
| 24 | 3328.0 | 3328.0 | 3328.0 | 131.370982 |
| 25 | 3456.0 | 3456.0 | 3456.0 | 138.763456 |
| 26 | 3584.0 | 3584.0 | 3584.0 | 149.113421 |
| 27 | 3712.0 | 3712.0 | 3712.0 | 141.297511 |
| 28 | 3840.0 | 3840.0 | 3840.0 | 138.413021 |
| 29 | 3968.0 | 3968.0 | 3968.0 | 145.961642 |
| 30 | 4096.0 | 4096.0 | 4096.0 | 153.919412 |
Download Jupyter notebook: 03-matrix-multiplication.ipynb